Magické čtverce obsahují n × n polí, kde je vepsáno n2 čísel. Magický čtverec řádu n vytvoříme umístěním přirozených čísel 1 až n2 do čtverce tak, že se každé z čísel ve čtverci vyskytuje právě jednou a součet čísel v každém sloupci, řádku a úhlopříčce je stejný. Součty v řádcích, sloupcích a diagonálách jsou stejné a nazývají se konstanta čtverce. Ta se dá určit podle vzorce pro součet prvních několika členů aritmetické posloupnosti 1, 2, …, n2
![]()
Pokud slevíme z některého požadavku pro magické čtverce, tak získáme další zajímavé čtverce, např. pozoruhodné čverce (platí podmínka pro stejný součet sloupců a řádků), latinské čtverce (do čtverce n×n se vpisuje jen 1, 2, …, n čísel, které se neopakují v žádném řádku ani sloupci) nebo čtverce tvořené prvočísly. Historie magických čtverců začala v 10. století, když se na ně poprvé matematici začali dívat jako na matematických objekt. Dřív byl magický čtverec brán spíš jako cosi tajemného a v některých případech byl používán i jako talisman. V minulosti se této oblasti věnovala řada významných matematiků, např. Luca Pacioli, Michael Stifel, Leonhard Euler, Girolamo Cardano, Pierre Fermat, Benjamin Franklin.
Jako latinský čtverec řádu n se označuje čtvercová tabulka, ve které je umístěno n znaků tak, aby v každém řádku a sloupci byly navzájem různé znaky.

Leonhard Euler zavedl latinské čtverce jako nový druh čtverců magických. Na rozdíl od nich se tu nepoužívá žádná aritmetická operace, a navíc místo čísel tu mohou být jakékoliv symboly. Označní čtverců jako latinských je proto, že se používaly písmena latinky.
Magický čtverec řádu dva neexistuje. Pokud by existoval, byl by třeba ve tvaru
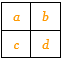
A platilo by, že a + b = a + c, tedy že b = c a to je v rozporu s pravidly pro tvorbu magických čtverců.
Magický čtverec s nejmenším řádem je tři, jehož konstanta je 15. Tento magický čtverec existuje jediný, ale dalších sedm verzí lze sestavit z jeho rotací nebo souměrností. Příkladem může být tento magický čtverec.
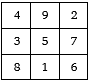
Podle staré čínské pověsti měla právě tento magický čtverec s názvem Luo Šu na zádech vyrytý želva, která se vynořila z řeky Luo. Čtverec s názvem Luo Šu byl v Číně znám již v době kolem roku 3000 před n. l.
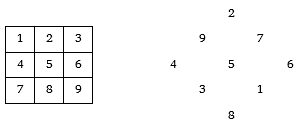
Při konstrukci magického čtverce řádu tři zapíšeme do tabulky postupně čísla 1 až 9. Vyměníme pozici číslic na diagonálách, tady 1 – 9, 3 – 7 a čtverec zapíšeme diagonálně. Nyní můžeme sestavit čtyři různé magické čtverce rotací kolem středu, čtyři jako osové souměrnosti.
Další metodu konstrukce čtverce 3×3 nalezl na konci 17. století Simon de la Loubére, francouzský velvyslanec u siamského krále. Jeho metoda funguje pro čtverce s lichým počtem sloupců a řádků. Nejprve se umístí 1 do středu prvního řádku a pak se postupuje šikmo vpravo nahoru. Pokud je políčko obsazeno, posuneme se o jedno políčko dolů.

Roku 1514 vložil Albrecht Dürer magický čtverec řádu 4 do kompozice své mědirytiny Melancholie nad postavu anděla. Dürerův magický čtverec je historicky i prvním narozeninovým magickým čtvercem vůbec. Rok vzniku mědirytiny (1514) udávají dvě prostřední pole v posledním řádku. Dürer ho sestrojil pro n = 4 a konstantou čtverce 34. Údajně se jedná o první magický čtverec, který se objevil v Evropě.
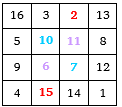
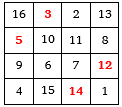

Všude dostaneme součet 34 i po přehození řádků a sloupců dostaneme ďábelský čtverec.
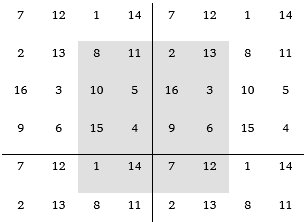
Pro n = 5 existuje 2 202 441 792 magických čtverců, 28 800 ďábelských čtverců. Ďábelské čtverce řádu 6 neexistují.
Benjamin Franklin se v mládí zabýval sestavováním magických čtverců. Byl v tom mistr. Zde je jeden z nich, který vyniká různými souměrnostmi, a proto se nazývá supermagický: součet čísel v řádích, sloupcích, úhlopříčkách, ale i v zalomených řádcích je 260, ve středním čtverci 2×2 i v rozích je 130 (polovina z 260).
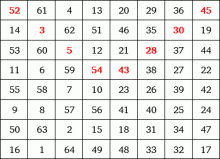
Existují magické čtverce tvořené druhými mocninami, ale jen o velikosti 4×4 nebo 5×5. Magický čtverec tvořený druhými mocninami o velikosti 3×3 nebyl zatím objeven. Existuje několik příkladů, které se v jednom nebo dvou číslech liší od druhých mocnin jen nepatrně. Příklad magického čtverce 4×4 našel Leonhard Euler v roce 1770 a zaslal ho v dopise Josephu Lagrangeovi. Jeho magickou konstantou je číslo 8 515. Podnítil tak rozvoj řady matematických problémů, které se řeší i v současnosti.
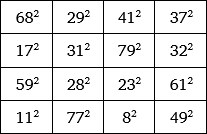
Christian Boyer nalezl magické čtverce tvořené druhými mocninami o velikosti 4×4, 5×5 a dokonce 7×7. V případě čtverce 7×7 dokonce existuje magický čtverec tvořený druhými mocninami čísel od 0 do 48.
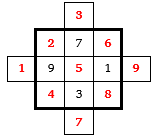
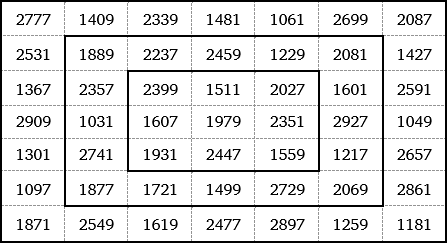
Další zajímavou variantou magického čtverce je ten tvořený samými prvočísly. Allan Johnson, jr. nalezl magický čtverec o velikosti 7×7 tvořený samými prvočísly. Navíc je rámovaný tzn., že všechny menší čtverce jsou také magické.
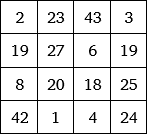
Do magického čtverce můžeme vepsat třeba datum narození, pak hovoříme o narozeninovém magickým čtverci. První takový vytvořil Albrecht Dürer v mědirytině Melancholie, kam vepsal rok vzniku mědirytiny 1514. Pokud upustíme od podmínek, že čtverec musí být tvořený po sobě jdoucími čísly a každým číslem jen jednou, můžeme k sestavení narozeninového čtverce použít následující pravidlo. Datum narození je A. B. CD, kde A je den, B měsíc a CD rok.

Jako příklad uveďme čtverec s datem vzniku toho článku – 27. 6. 2018. Pak konstanta magického čtverce je 71 a čtverec vypadá takto.
Použité zdroje:
[1] BÁLINTOVÁ, A. – TROJÁČKOVÁ, R. Sudoku a história magických štvorcov. Sborník sylabů 31. mezinárodní konference historie matematiky, Velké Meziříčí 18. – 22. 8. 2010. Matfyzpress, Praha 2010.
[2] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[3] FUCHS, E. Magické čtverce aneb Od Knihy I-t´ing k internetové současnosti.
[4] PRADLOVÁ, J. O čem přemýšlí Dürerův anděl aneb magický čtverec z Fibonacciho čísel. Matematika-Fyzika-Informatika. Roč. 11, únor 2002, č. 8, s. 321-328.
[5] SPENCER, A. Kniha čísel. 1. vydání. Praha: Albatros, 2005. ISBN: 13-805-KMČ-005.
[6] STEWART, I. Kabinet matematických kuriozit profesora Stewarta. Praha: Dokořán, 2013. ISBN 978-80-7363-292-2.
[7] STEWART, I. Truhlice matematických pokladů profesora Stewarta. Praha: Dokořán, 2013. ISBN 978-80-7363-527-5.