Číselné soustavy

Číselná soustava představuje způsob, jak zapisovat čísla pomocí znaků – číslic. Různé kultury si v různých dobách osvojily rozmanité metody zápisu čísel, ale většina dnešních numerických systémů je založena na deseti, což je počet prstů na rukou. Výjimkami byli Mayové, Aztékové a Keltové, kteří měli dvacítkové soustavy, protože počítali prsty na rukou i nohou. Základ číselné soustavy zřejmě vznikl v době, kdy si člověk potřeboval spočítat třeba státo ovcí. Pokud jich měl 598 a uměl počítat jen do deseti (deset prstů) mohl počítat třeba takto: za každých napočítaných deset ovcí odložil jeden kamínek. Na konci měl tedy 59 kamínků a osm prstů. Do 59 ale počítat neuměl a tak teď počítal kamínky a za každých deset odložil stranou jeden list. Nakonec napočítal 5 listů, 9 kamínků a 8 prstů. Odtud už byl jen krůček k jinému pojmenování listů, kamínků a prstů.

Požiční číselné soustavy

Sumerové a Babyloňané zhruba před 4000 lety používali v běžném životě poziční soustavu. Poziční jí říkáme proto, že hodnotu zapsaného čísla určují pozice jednotlivých znaků. Základem jejich soustavy bylo číslo 60 – čísla tedy zapisovali v šedesátkové soustavě. Jako pozůstatek této soustavy používáme šedesátkovou soustavu pro počítání času a při měření úhlů.

Nejstarší čínské zápisy čísel se objevují na magických kostkách ze 14. až 11. století před n. l. a na keramických a bronzových předmětech a mincích z 10. až 3. století před n. l. Od 4. století před n. l. a možná i dříve používali Číňané k vyjádření čísel tyčinky, jejich používání se udrželo až do 13. století. Používali 18 znaků pro čísla 1 až 9 a pro desítky od 10 do 90. Jedná se o nejstarší destítkovou poziční soustavu.

Čínské znaky pro čísla.
Zdroj: FRANCOVÁ, L. Vývoj číselných soustav. Elektronický studijní materiál projektu CenTal.

Symboly pro jednotky označovaly také stovky, desítky tisíce atd. Neexistoval symbol pro nulu. Při zápisu se jednoduše vynechalo místo. Symbol pro nulu se do Číny dostal později z Indie.

Zápis čísla 6728.
Zdroj: FRANCOVÁ, L. Vývoj číselných soustav. Elektronický studijní materiál projektu CenTal.

Dnešní poziční desítková soustava, kterou později propracovali Indové, vychází z babylonské šedesátkové soustavy. Výhody poziční desítkové soustavy spočívají ve způsobu, jakým lze pomocí ní psát velmi velká i velmi malá čísla. Desítková indická soustava vznikla v 6. až 8. století. Tento systém se rozšířil prakticky po celém světě. Protože tuto soustavu rozšířili Arabové, nazývá se tato soustava arabská. Do Evropy se dostala až v polovině 10. století, ale trvalo 600 let než ji lidé zvládli.

Zápis čísla v poziční soustavě se opírá o tuto větu: každé přirozené číslo a lze v poziční číselné soustavě vyjádřit ve tvaru

O čísle a_i se říká, že je číslicí (cifrou) řádu i čísla a. Číslo z se nazývá základ soustavy. Nejrozšířenější číselnou soustavou je desítková, kde je z = 10 a každé číslo je zapsáno ve tvaru

Jednotky některých řádů desítkové soustavy mají speciální názvy: deset, sto, tisíc, milion, miliarda (10⁹), bilion (10¹²), trilion (10¹⁸). Podobným způsobem můžeme zapisovat zlomky a desetinná čísla. Použijeme k tomu záporných mocnin čísla 10 nebo jiného základu (například 0,104 = (0,023)₅).

Existují i jiné poziční číselné soustavy, např. dvojková, dvacítková, šedesátková. U soustav, kde je základ větší než deset nestačí deset číslic, proto se v zápisu používají velká písmena A, B, C. Počítače používají dvojkovou soustavu, která má základ dvě číslice 0, 1. Každé přirozené číslo a lze vyjádřit právě jedním způsobem ve tvaru

Například číslo 56 přepíšeme nejprve pomocí mocnin dvou: 56₁₀ = 32 + 16 + 8 = 1.2⁵ + 1.2⁴ + 1.2³ + 0.2² + 0.2¹ + 0.2⁰ = 111000₂. Dvojkovou soustavu člověk používá i jinde. Je to Morseova abeceda, která písmena a číslice vyjadřuje pomocí dvou znaků – tečky a čárky.

Nepoziční číselné soustavy

Mezi nepoziční soustavy patří např. egyptská nebo římská číselná soustava. Egypťané používali sedm základních číselných znaků pro jednotlivé řády. Základním číslem soustavy je číslo 10 – jedná se tedy o soustavu desítkovou.

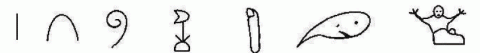
Egyptské symboly pro čísla (zleva-doprava): patrně měřící hůl označuje 1; kraví pouta na nohy označují 10, stočený měřící provazec k vyměřování polí označuje 100; květ lotosu označuje 1000; ukazovák představuje 10 000; pulec představuje 100 000 a některý z bohů představuje číslo 1 000 000.
Zdroj: FRANCOVÁ, L. Vývoj číselných soustav. Elektronický studijní materiál projektu CenTal.

Jednotlivá přirozená čísla pak zapisovali opakováním těchto znaků.

Zápis čísla 2 465 (nahoře) a 2 123 013.
Zdroj: FRANCOVÁ, L. Vývoj číselných soustav. Elektronický studijní materiál projektu CenTal.

Další nepoziční a velmi zajímavou číselnou soustavu používali Mayové. Používali dvacítkovou soustavu. Pomocí teček a čárek znázorňovali čísla od 1 do 20. Jestliže byla pod číslem zakreslena škeble, vyjadřovala dvacetinásobek původní hodnoty. Pokud číslo končilo jinou číslicí než 0, pak se znak škeble vynechal.

Mayský zápis čísel.
Zdroj: DEPMAN, I. – FOLTA, J. Svět čísel. Vyprávění o matematice. Praha: SPN, 1973. ISBN: 14-513-73.

Další nepoziční číselnou soustavou je ta římská, která není čistě desítkovou soustavou, ale kombinací pětkové a desítkové soustavy. Římané převzali tuto soustavu od Etrusků. K zápisu byly původně používány speciální znaky, které byly ve středověku přeměněny do dnešní podoby. Přirozená čísla se v ní zapisují pomocí římských číslic představovaných sedmi znaky

• znaky se skládají psaním od znaků pro nejvyšší hodnoty k nejnižším (MDL = 1550)
• většinou se kombinují nejvýše 3 stejné číslice (XXX = 30, III = 3). Někdy mohou být kombinovány i čtyři stejné číslice (IIII = 4 bylo běžné na starých slunečních hodinách)
• čísla zapsaná stejnými znaky vedle sebe se sčítají
• je-li znak menšího čísla napsán za znakem většího čísla, pak obě tato čísla se sčítají
• je-li znak většího čísla napsán za znakem menšího čísla, pak od většího čísla se odečítá menší číslo
• pro odečítání se používají pouze znaky IXC, použití VLD je nepřípustné (pro zápis VC = 95 není správný)
• znak I zpravidla odečítáme jen od V a X
• znaky IXC se mohou za sebou opakovat nejvýše třikrát; znaky V, L, D se v každém čísle vyskytují nejvýše jednou; znak M se může opakovat libovolněkrát.

Římská čísla vznikla přirozenou cestou. Římané počítali na prstech. Čísla jako 1, 2, a 3 a jím odpovídající znaky I, II a III graficky vyjadřují jednotlivé prsty. I původ dalších dvou znaků V a X je v lidské ruce - X jsou dvě dlaně u sebe (10 prstů).

Odvození římských číslic.
Zdroj: commons.wikimedia.org. Public domain.

Označení dalších čísel pochází z latinského centum – sto, odtud C. Padesát je polovina ze stovky. L tedy vzniklo "rozpůlením" znaku pro 100 (C). Znak pro tisíc pochází z latinského mille (odtud M pro 1000). Znak D pro 500 vznikl opět grafickým "půlením" znaku M, tentokrát svisle. Vznikl tak znak podobný písmenu D.

Použité zdroje:

[1] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.

[2] CRILLY, T. Velké otázky. Matematika. Praha: Knižní klub, 2012. 1. vydání. ISBN: 978-80-242-3596-7.

[3] DEPMAN, I. – FOLTA, J. Svět čísel. Vyprávění o matematice. Praha: SPN, 1973. ISBN: 14-513-73.

[4] FRANCOVÁ, L. Vývoj číselných soustav. Elektronický studijní materiál projektu CenTal. [online]. [cit. 2017–12–12]. URL: http://black-hole.cz/cental/wp-content/uploads/2010/10/V%C3%BDvoj-%C4%8D....

[5] HAVIGER, J. Racionální čísla z pohledu číselných soustav. Učitel matematiky, říjen 2007, roč. 16, č. 1 (65), s. 18–31. ISSN 1210–9037.

[6] MRÁZEK, J. Taje matematiky. Praha: Práce, 1986. ISBN 24-025-86.

[7] MRÁZEK, V. Číselné soustavy v osnovách středních odborných škol. Matematika ve škole, roč. 13, 1962/63, s 25-31. Praha: SPN.

[8] MÜLLEROVÁ, J. Matematika pro 7. ročník 1. díl. Praha: Státní pedagogické nakladatelství, 1990. ISBN 80-04-24008-9.