Ať si v nich libujeme nebo je nenávidíme, čísla nás provázejí od kolébky ke hrobu. Potřebu počítat pocítil člověk ještě dříve než touhu psát. Historie zapisování a vyjadřování čísel je velmi dlouhá a složitá. Člověk nejprve počítal prsty na rukou, když mu nestačily, použil i prsty u nohou. Označení prstů a číslovek bylo (a u řady primitivních národů je) podobné. Často je číslo pět vyjádřeno slovem ruka nebo pěst, deset jako dvě ruce, dvacet jako člověk. Už Aristoteles přišel s tím, že základ používaných číselných soustav souvisí s počtem prstů. Podle různých teorií začali lidé používat čísla v primitivní písemné podobě asi před 30 000 lety. První formou byl zápis pomocí unárního systému, ve kterém je každé číslo reprezentované odpovídajícím počtem zvolených symbolů, např. zářezů na vrubovkách.Jako vrubovky se označují dřevěné hůlky nebo kosti se značkami. Nejstarší vrubovka pochází z doby před 37 000 lety a má podobu 29 vrubů vytesaných do kosti z nohy paviána. Kost byla nalezena v jeskyni v horách Lebombo v Africe. Shruba 30 000 let je stará vlčí kost s 57 vruby, která byla nalezena na našem území. V podstatě se tento systém používá dodnes, např. při záznamu karetních výher nebo v restauracích.
Indové používali největší čísla ve své době. Měli, i na dnešní dobu, nejrozsáhlejší číslovkovou soustavu. Měli zvláštní výraz pro jednotky až sedmnáctého řádu. V prastaré indickém eposu Mahábhárata se hovoří o 600 000 milionů Buddhových synů a o 24 ∙ 1015 bozích. Jedna z tehdejších lidových pohádek vypráví o bitvě, které se zúčastnilo 10 000 sexilionů opic (= 1040) nebo králově jmění 100 000 bilionů (=1016). Indové dokonce dospěli až k číslu 104352. Velkými čísly se zabýval i Archimedes, který se ve spisu Počítání písku snažil pomocí velkých čísel zapsat počet zrn písku na Zemi. Dospěl tak k číslu 1063. I v současnosti se používají velká čísla. Některá mají dokonce své názvy, je to třeba milion (106), miliarda (109), bilion (1012) atd. Ale co třeba 10100? Tak i toto ohromné číslo má svůj název, který v roce 1938 vymyslel Milton Sirotta a je to googol. Existuje ale pojmenování pro ještě větší číslo. Je to 10googol a jmenuje se googolplex.
Dnešní zápis čísel pomocí číslic pochází od Indů. Od nich je Rihan Muhamed ebn Alibiruni přinesl do Arábie. Arabové přeložili indické slovo označující nulu jako as-syfr a z toho pochází naše slovo cifra. Od Arabů je poznali v devátém století italští kupci a ti je pak přinesli do Evropy. Další možností je, že učený španělský mnich Gerbert (papež Sylvestr II.) v roce 999 poznal tyto číslice u Arabů a z jeho spisů se rozšířily v desátém a jedenáctém století do Evropy. První evropský spis o indických číslicích a počítání s nimi vydal počátkem devátého století Abú al–Chwárizmí s názvem Algoritmi de numero Indorum. Zavedení do praxe probíhalo jen zvolna. První latinský spis Liber abaci o indických číslicích napsal Leonardo Pisánský v roce 1202. K všeobecnému rozšíření indických číslic došlo až v patnáctém a šestnáctém století.
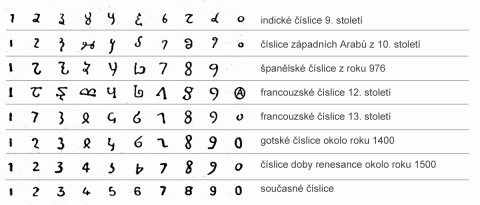
Vývoj číslic.
Zdroj: DEPMAN, I. Besedy o matematice. Praha: Státní pedagogické nakladatelství, 1957.
Speciálním číslem je nekonečno, pro které se používá symbol ∞. Ten zavedl v roce 1650 John Wallis. Možná byl odvozen z ω, posledního písmene řecké abecedy. Možná ale ne. Jeho skutečný původ je neznámý.
Použité zdroje:
[1] CRILLY, T. Velké otázky. Matematika. Praha: Knižní klub, 2012. 1. vydání. ISBN: 978-80-242-3596-7.
[2] FABINGER, F. O vývoji čísel, číslovek, číslic. Časopis pro pěstování mathematiky a fysiky. 1903, roč. 32, s. 249–259. 1904, roč. 33, s. 74-93.
[3] FRANCOVÁ, L. Vývoj číselných soustav. Elektronický studijní materiál projektu CenTal. [online]. [cit. 2017–12–12]. URL: http://black-hole.cz/cental/wp-content/uploads/2010/10/V%C3%BDvoj-%C4%8D....
[4] GOLDSMITH, M. Od nuly k nekonečnu. Matematické vychytávky, které musíš znát. Praha: Fortuna, 2013. ISBN 978-80-7321-717-4.
[5] MRÁZEK, J. Taje matematiky. Praha: Práce, 1986. ISBN 24-025-86.
[6] PORUBSKÝ, Š. Dokonalé čísla. Najstarší otvorený problém matematiky. 29. mezinárodní konference Historie matematiky, Velké Meziříčí, 22. 8. – 26. 8. 2008, s. 33–48 1. vydání. Praha: Matfyzpress, 2008. ISBN 978-80-7378-048-7.

