Fibonacciho čísla tvoří snad nejslavnější posloupnost pojmenovanou po Fibonaccim nebo-li Leonardu Pisánském. Ten tuto posloupnost popsal ve svém díle Liber Abaci z roku 1202 na problému s množením králíků: „Na pole umístíme pár králíků. Jestliže králíci po měsíci dospějí a zplodí každý měsíc nový pár – kolik párů králíků se narodí za dvanáct měsíců?“ Řešením je číslo 144, které je dvanáctým členem posloupnosti čísel 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ... Ta počínaje třetím členem vzniká tak, že další člen je součtem dvou předchozích členů. Tato posloupnost čísel byla známá už dříve v Indii.
Fibonacci. Zdroj: commons.wikimedia.org. Public domain.
Vždy dvě po sobě jdoucí Fibonacciho čísla nejdeme ve spirálách např. šišky (podle velikosti 8 spirál po směru a 13 proti směru, 5 po směru a 3 protisměru), květu slunečnice (34 po směru a 21 proti směru nebo 34 a 55, 55 a 89, 89 a 144) nebo ananasu (existují tři druhy spirál po 8, 13 a 21). Tuto vlastnost (fylotaxe) můžeme pozorovat i u jiných květů, plodů nebo uspořádání listů na větvi (při pohledu shora).
Nejprve si ale vysvětleme, co to ta posloupnost vlastně je. Je to funkce, jednodušeji nějaké pravidlo, které přiřazuje prvnímu, druhému, třetímu, obecně n-tému členu určitou hodnotu. Posloupnosti můžeme zadat přímo jednotlivými členy, vzorcem pro n-tý člen, tabulkou, graficky nebo rekurentně. První případy jsou známé, vysvětleme si ten poslední. Rekurentně (z lat. recurrere – běžet zpět) je posloupnost zadaná pomocí několika prvních členů a předpisu, podle něhož můžeme vypočítat členy další. Mezi nejznámější posloupnosti patří posloupnost aritmetická, kde každý další člen získáme přičtením stejného čísla (např. 2, 5, 8, 11, 14, 17, …), a posloupnost geometrická, kde každý další člen získáme vynásobením stejného čísla (3, 6, 12, 24, 48, …).
Fibonacciho posloupnost můžeme zadat obecně pomocí rekurentního vzorce an+2 = an+1 + an, kde zvolíme za a1 = a a a2 = b, kde čísla a a b jsou různá od nuly. Několik prvních členů zobecněné Fibonacciho posloupnosti pak je a, b, a + b, a + 2b, 2a + 3b, 3a + 5b, … Pokud zvolíme a = 1, b = 1 získáme Fibonacciho posloupnost, pokud zvolíme a = 1, b = 3 pak získáme Lucasovu posloupnost, jejíž členy se nazývají Luccasova čísla.
Určité vědomosti o posloupnostech lze vysledovat již ve starém Egyptě a Babylóně. V Ahmesově papyru (asi 2 000 před n. l.) je uvedena tato úloha: "Sto měr zrní je třeba rozdělit pěti dělníkům tak, aby druhý dělník dostal o tolik měr více než první, o kolik třetí dostal více než druhý, čtvrtý než třetí a pátý než čtvrtý. Kromě toho mají první dělníci dohromady dostat sedmkrát méně měr zrní než ostatní tři“. Zajímavé úlohy o posloupnostech jsou ve staročínské Matematice v devíti knihách (2. stol před n. l.). V knize VII lze např. najít tuto úlohu: "Klusák a herka vybíhají z jednoho místa v témž směru. Klusák proběhne za první den 193 li (li je staročínská jednotka délky), každý následující den o 13 li více. Herka uběhne za první den 97 li a každý den o polovinu méně. Po proběhnutí 3 000 li se klusák vrací a na zpáteční cestě potkává herku. Ptáme se, za kolik dní se setkají a jakou dráhu uběhne každý z nich." Řešení těchto a podobných úloh je ve starých matematických knihách těžkopádné a ne příliš elegantní. Chybějí potřebné vzorce, nejsou k dispozici jednoduché zápisy ani vhodná terminologie.
Značná pozornost byla věnována posloupnostem ve starém Řecku. Pythagorejci např. uměli vyjádřit součet prvních n přirozených čísel, součet prvních n lichých (sudých) čísel, Euklides v 9. knize Základů uvedl vzorce pro součet prvních n členů geometrické posloupnosti. V Řecku se setkáváme i s úvahami o nekonečných řadách. Posloupnosti zajímaly i indické matematiky. Pro ilustraci uvedeme jednu úlohu pocházející ze 14. století: "Je třeba vypočítat počet krav ve stádu, jež získáme od jedné krávy za 20 let, víme-li, že se každé krávě narodí počátkem každé roku jedno tele a každé tele dává stejné potomstvo, jakmile dosáhne věku tří let." Středověk se o vývoj této části matematiky nijak podstatně nezasloužil. Teprve od 17. století dochází k rozvoji teorie posloupnosti.
V souvislosti s aritmetickou posloupností se vypráví historka o malém Karlu Gaussovi. Když byl Gauss malým žáčkem, zadal jeho učitel při hodině matematiky namáhavý a dlouhý úkol – chtěl děti na delší dobu zabavit, a tak měli vypočítat součet všech celých kladných čísel od 1 do 100. Gauss prý ale vzápětí prohlásil „Je to 5 050.“ Učitel se ho užasle zeptal, jak na to přišel? Malý Gauss odpověděl, že sečetl první a poslední číslo vynásobil to počtem číslic a vydělil dvěma.
Vraťme se zpátky k Fibonacciho posloupnosti. Fibonacciho čísla mají úzký vztah ke zlatému číslu, jehož hodnota je přibližně
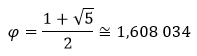
Vzájemné poměry dvojic po sobě jdoucích Fibonacciho čísel, tedy zlomky 2/1, 3/2, 5/3, 8/5, 13/8, 21/13 atd. se postupně s rostoucím n blíží ke zlatému číslu. Jinak řečeno posloupnost Fn+1/Fn má pro n jdoucí k nekonečnu limitu rovnou φ. Dokonce existuje vzorec pro n-té Fibonacciho číslo vyjádřený pomocí čísla φ:
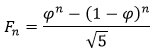
Odtud plyne, že Fn musí být celé číslo, které je danému zlomku nejbližší.
Pokud postupně sestrojíme čtverce o stranách s délkami rovnými Fibonacciho číslům, tak je možné je hezky poskládat vedle sebe. Pokud načrtneme v každém z nich čtvrtkružnici, tak nám vznikne Fibonacciho spirála, která je díky spojitosti s číslem φ podobná logaritmické spirále.
Fibonacciho spirála.
Zdroj: commons.wikimedia.org. Under Creative Commons.
Použité zdroje:
[1] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[2] JAROŠOVÁ, M. Fibonacciho čísla a důkazy beze slov. Setkání učitelů matematiky všech typů škol. Srní 2010.
[3] SPENCER, A. Kniha čísel. 1. vydání. Praha: Albatros, 2005. ISBN: 13-805-KMČ-005.
[4] STEWART, I. Kabinet matematických kuriozit profesora Stewarta. Praha: Dokořán, 2013. ISBN: 978-80-7363-292-2.0.
[5] ZDEBOROVÁ, L. Květ slunečnice a Fibonacciova čísla. Rozhledy matematicko–fyzikální, roč. 82 (2007), č. 1, s. 1-10. ISSN 0035-9343.
