Číslo π (od slova periféria – obvod nebo perimetron – měření kolem) představuje poměr délky kružnice ku jejímu průměru. Poprvé symbol π ve smyslu obvodu kruhu použil William Oughtred v roce 1647 nebo Isaac Barrow v roce 1664. V roce 1706 použil symbol π William Jones ve významu poměru obvodu kruhu ku jeho průměru. Všeobecně se tento symbol začal používat od roku 1748, kdy Leonhard Euler vydal Úvod do analýzy nekonečna, kde toto označení používal. Toto číslo se někdy označuje jako ludolfovo na počest holandského matematika Ludolfa van Ceulena, který v roce 1610 jeho hodnotu vypočetl na 35 desetinných míst. K výpočtu použil Archimedovu metodu s mohoúhelníkem o 10 473 741 248 stranách.
A jaká je tedy hodnota čísla π? S přesností na třicet desetinných míst je to 3,141 592 653 589 793 238 462 643 383 279. K zapamatování prvních několika desetinných míst čísla π nám může pomoci stará mnemotechnická pomůcka ve formě básničky, přičemž počet písmen každého slova udává příslušnou číslici.
Lín a kapr u hráze
prohlédli si rybáře
udici měl novou
jikrnáči neuplovou.
Nebo
Sám u sebe v hlavě
magického pí číslic deset mám.
Nebo
Mám ó Bože ó velký
pamatovat si takový cifer řád,
velký slovutný Archimedes,
pomáhej trápenému,
dej mu moc,
nazpaměť nechť odříká ty slavné sice,
ale tak protivné nám, ach, číslice Ludolfovy!
Dalším zajímavým problémem týkajícím se čísla π je otázka, zda se v desetinném rozvoji vyskytují všechna čísla a všechny číselné kombinace se stejnou pravděpodobností. Ze zatím zjištěných desetinných míst se však žádné nápadnosti nevyskytují. Musí se tedy někdy objevit třeba i kombinace 999 999 (šesti devítek jdoucích po sobě) To si také řekl Richard Feynman a prohlásil, že se naučí všechna desetinná místa čísla π až do kombinace šesti devítek. Od té doby se toto místo, které začíná na 762. místě za desetinnou čárkou, nazývá Feynmanův bod. Zda se to Richard Feynaman naučil dnes přesně nevíme. Zato rekord v bezchybném vyjmenování 22 514 desetinných míst čísla π drží Daniel Tammet z roku 2004.
Přesnou hodnotu čísla π nikdy nezjistíme, protože v roce 1768 Johann Lambert dokázal jeho iracionalitu. Přesto se můžeme pokusit o výpočet jeho přibližné hodnoty. Ferdinand von Lindemann dokázal, že číslo π je transcendentní, tzn. že nemůže být kořenem žádné alegebraické rovnice. Tím také vyřešil dávný problém označovaný jako kvadratura kruhu – úlohu, která má za úkol převést daný kruh na čtverec o stejném obsahu jen s pomocí pravítka a kružítka. Lindemann tak prokázal její neřešitelnost.
My ale vlastně přesnou hodnotu čísla π nepotřebujeme. Pokud budeme počítat s přesností na milimetry, pak si vystačíme s hodnotou 3,14. Pokud ale budeme počítat s velkými vzdálenostmi odpovídajícími rozměrům sluneční soustavy, tak nároky na přesnost budou narůstat. Stále nám ale bude stačit asi oněch třicet míst uvedených v z předchozích odstavců. Řadě lidí to však nestačí, a tak se snaží vypočítat hodnotu čísla π na co největší počet míst. V tom jim dnes pomáhají počítače.
Výpočet čísla π
Nejstarší, když velmi hrubý odhad hodnoty čísla π = 30/10, najdeme už na stránkách Starého zákona. Některé výzkumy ukazují, že hebrejská písmena v určitých opisech lze číst i jako jiné číslice a π by pak mělo hodnotu
![]()
Někdy bývá používána jako aproximace π hodnota 3√31. Ve starém Egyptě se používala hodnota √10, jak se píše v Rhindově papyru z roku 1700 před n. l. V 5. století zjistil slavný čínský astronom Tsu Ch´ung-Chih, že vezmeme-li tři páry prvních lichých čísel 1-1, 3-3, 5-5 a napíší se poslední tři do čitatele zlomku a první tři do jeho jmenovatele, dostaneme zlomek 355/113. Ten odpovídá hodnotě čísla π na šest desetinných míst přesně. Další přesnější aproximace jsou 103993/33102 nebo 104348/33215.
Nejstarší metoda výpočtu čísla π pochází od Archiméda. Je založena na myšlence, že vepíšeme-li do dané kružnice libovolný mnohoúhelník, bude jeho obvod menší než délka kružnice; pokud naopak kolem kružnice mnohoúhelník opíšeme, bude jeho obvod větší než délka kružnice. Archimedes správně usoudil, že zvětšováním počtu stran mnohoúhelníku se jeho obvod více blíží délce kružnice. Použil proto pravidelné mnohoúhelníky s 12, 24, 48 a 96 stranami a tak dostal pro číslo π dolní a horní hranice.

Všeobecně se udává Archimédovo vyjádření čísla π jako 3 1/7.
Archimédovu metodu několik století zlepšovali a upravovali. Místo vepsaných a opsaných mnohoúhelníků se např. uvažovalo o mnohoúhelnících s dvojnásobným počtem stran s tímtéž obvodem nebo obsahem apod. Tyto výpočty mají nyní jen historický význam, neboť s rozvojem matematické analýzy se našlo mnoho vzorců a způsobů, jak o mnoho přesněji a rychleji vypočítat číslo π.
Francouzský matematik Francois Viete v roce 1593 poprvé vyjádřil číslo π jako matematický vzorec, který ale odvodil z geometrie.

nebo
![]()
Další možnost výpočtu čísla π se do historie zapsal jako Basilejský problém a jeho počátek sahá až do roku 1644, kdy se Pietro Mengoli ptal, zda dostaneme konečnou hodnotu, když sečteme převrácené hodnoty druhých mocnin přirozených čísel. Název Basilejský je podle místa, které se k jeho řešitelům váže. Problém se snažilo vyřešit několik členů slavné rodiny Bernoulliů, ale úspěšný byl až Leonhard Euler (mimochodem narozený v Basileji), který dokázal, že pro součet předchozí řady platí
![]()

Podle Wilhelma Gottfrieda Leibnitze nebo Jamese Gregoryho, kteří vztah objevili zároveň kolem roku 1675, je
![]()
Tento vzorec vychází z řady
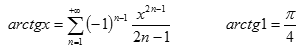
Pro takový výpočet je třeba velmi mnoho trpělivosti, neboť abychom získali šestimístné číslo, je třeba vzít v uvedené řadě dva miliony členů.
Podle Johna Wallise můžeme π vypočítat podle vzorce z roku 1655
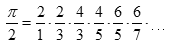
nebo

V 17. století odhalil lord Brounsker řetězový zlomek
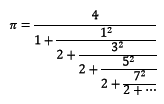
Dále se π dá vypočítat jakou součet následujících řad
![]()
ale tady je třeba sečíst velké množství členů.

Eulerova řada
![]()
nebo jako limita funkcí (tzv. Stirlingův vzorec)
![]()
anebo již podle zmíněného Wallise (v jiném tvaru):

Srinivasa Ramanujan vymyslel pro výpočet čísla π několik aproximačních vzorců, např.
![]()
nebo o něco složitější z roku 1985, který obejvili Jonathan a Peter Borweinovi
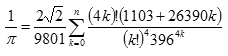
V současné době se k výpočtu desetinných míst čísla π používají počítače. Jedním z možných postupů je a0 = 6 - 4√2, y0 = √2 – 1 a postupně dosazujeme do vztahů
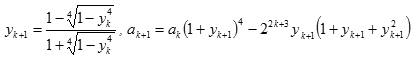
Pak ak konverguje velmi rychle k číslu 1/π. V roce 1983 byla tato metoda použita na 16kB počítači pro 21 iterací. V roce 1986 byla použita na počítači Cray-2 v NASA pro výpočet 29,4 milionu platných číslic. Výpočet trval 40 hodin. V lednu 2009 bylo touto metodou vypočteno 1,649 miliard číslic na počítači ApproXtreme X3. Výpočet trval 73,5 hodiny. V prosinci 2009 dosáhl Bellard 2,7 miliard číslic, výpočet trval 131 dnů. V srpnu 2010 pak bylo číslo π vypočítáno na 5 miliard číslic. Je velmi obtížné ověřit správnost výpočtu. Ta se provádí namátkovou kontrolou posloupností číslic zkoumaného číselného rozvoje.
V roce 1997 našli David Bailey, Peter Borwein a Simon Plouffe vzorec
![]()
S jehož pomocí je možné vypočítat číslici na určitém konkrétním místně rozvoje čísla π bez nutnosti výpočtu předchozích číslic. Jedinou nevýhodou vzorce je, že neudává desetinný rozvoj, ale hexadecimální (tedy o základu 16). V roce 1998 Fabrice Ballard pomocí tohoto vzorce zjistil, že stomilardtá číslice rozvoje čísla π je devítka.
Použité zdroje:
[1] BARTCH, H. Matematické vzorce. SNTL, Praha 1983
[2] CALDA, E. O Ludolfově číslu převážně vážně. Rozhledy matematiky a fyziky. Roč. 67, 1988-89, č. 5, s 177-179.
[3] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[4] CHAJDA, I. Jak vypočítat číslo π. Matematika-fyzika-informatika. Roč. 21, duben 2012, č. 8, s 461-463. ISSN 1210-1761.
[5] NOVOLESKÝ, Š. Zábavná matematika. Praha: SPN, 1974.
[6] STEWART, I. Kabinet matematických kuriozit profesora Stewarta. Praha: Dokořán, 2013. ISBN 978-80-7363-292-2.
[7] STEWART, I. Truhlice matematických pokladů profesora Stewarta. Praha: Dokořán, 2013. ISBN 978-80-7363-527-5.
[8] ŠIMŠA, J. Výpočet čísla π z obvodů pravidelných mnohoúhelníků. Rozhledy matematicko-fyzikální. Roč. 80, 2005. č. 1, s. 6-14, č. 2, s. 5-16.
[9] ŠOLCOVÁ, A. Číslo π a jeho přátelé. Rozhledy matematiky a fyziky. Roč. 65, 1986-87, č. 4, s. 153-161.
[10] ZIEGLER, G. Matematika vám to spočítá. Příběhy královny věd. Praha: Knižní klub, 2011. ISBN 978-80-242-3311-6.

