Prvočísla jsou všechna přirozená čísla, která mají právě dva různé dělitele, číslo jedna a samo sebe. Opakem jsou čísla složená, která mají aspoň tři různé dělitele. Toto rozdělní čísel zavedl Pythagoras. Číslo jedna nepovažujeme ani za prvočíslo, ani za složené číslo. Například číslo 40 není prvočíslo, protože je dělitelné 1, 2, 4, 5, 8, 10, 20 a 40. Ale číslo 41 je prvočíslo, protože je dělitelné 1 a 41. Prvočísla jsou základními kameny, ze kterých se staví všechna ostatní čísla. Proto jsou tak důležitá a jejich hlední se stále věnuje tolik času.
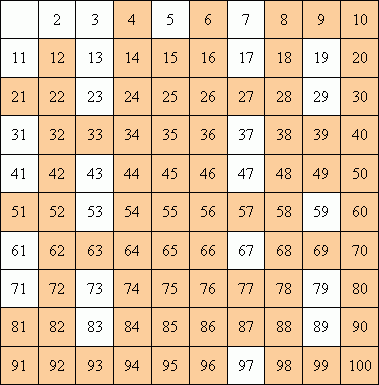
První čtyři prvočísla (2, 3, 5, 7) byla objevena už v dávnověku a další čtyři prvočísla (11, 13, 17, 19) se zachovala jako vruby na kosti z Ishanga. Kolik ale vlastně těch prvočísel je? Eratosthenes používal k vyhledávání prvočísel voskové tabulky s napsanými přirozenými čísly většími než jedna. Číslo dva ponechal a jehlou vypálil násobky dvou. Pak stejně postupoval s trojkou apod. Na konci výpočtu tabulka připomíná síto – tzv. Eratosthenovo síto.
Ze síta je vidět nutný (ne však dostačující) předpoklad, aby číslo bylo prvočíslem: musí končit číslicí 1, 3, 7 nebo 9. Jedinou výjimkou jsou prvočísla 2 a 5. Pokud chceme zjistit, zda je dané číslo prvočíslo, nemusíme zjišťovat, zda je dělitelné všemi prvočísli menšími. Stačí zjistit, zda je dělitelné pouze prvočísly menšími než jeho odmocnina. Zkoumáme např. číslo 211. Jeho odmocnina je asi 14,5. Stačí tedy zkontrolovat dělitelnost 211 čísly 2, 3, 5, 7, 11 a 13. Všechna tato dělení jsou se zbytkem, a proto číslo 211 je prvočíslem.
S prvočísly souvisí jeden z nedokázaných problémů označovaný jako Goldbachova hypotéza. Je pojmenovaný po Christianu Goldbachovi, který ho formuloval v polovině 18. století. Goldbachova hypotéza říká, že každé sudé číslo větší nebo rovno 4 se dá vyjádřit jako součet dvou prvočísel. Numericky byla hypotéza dokázána až do čísla 1018.
Euklides ve svých Základech (Kniha 9, tvrzení 20) dokázal, že prvočísel je nekonečně mnoho. Větu formuloval jako „prvočísel je víc než jakýkoliv počet prvočísel“. Základem důkazu jsou čísla dnes označovaná jako Eukleidova. Ta dostaneme tak, že vynásobíme všechna prvočísla až do daného prvočísla a k součinu přičteme jedničku.
|
Prvočíslo |
Výpočet |
Eukleidovo číslo |
|---|---|---|
|
2 |
2 + 1 |
3 |
|
3 |
3 ∙ 2 + 1 |
7 |
|
5 |
5 ∙ 3 ∙ 2 + 1 |
31 |
|
7 |
7 ∙ 5 ∙ 3 ∙ 2 + 1 |
211 |
|
11 |
11 ∙ 7 ∙ 5 ∙ 3 ∙ 2 + 1 |
2311 |
Eukleidova prvočísla jsou vzácná. Už pro 13 ho nedostaneme (13 ∙ 11 ∙ 7 ∙ 5 ∙ 3 ∙ 2 + 1 = 30031 = 59 ∙ 509). Další dostaneme až pro prvočíslo 31 (2 000 560 490 131), 379, 1019 nebo 1021.
Jednociferná jsou čtyři, dvojciferných je 21, trojciferných 143, čtyřciferných 1161, pěticiferných 8363 atd. Největší zatím známé prvočíslo má 12,9 milionu číslic.
Pokud leží na číselné ose mezi dvěma prvočísly jen jedno další číslo, pak se obě prvočísla nazývají prvočíselná dvojčata. Příkladem může být třeba 3 a 5, 5 a 7, 11 a 13 atd. Největší známá prvočíselná dvojčata jsou čísla 570 918 348 ∙ 105120 ∓ 1 objevená H. Dubnerem v roce 1994. Už ve starém Řecku se matematikové zabývali otázkou, zda takových prvočíselných dvojčat existuje nekonečně mnoho a jaká je jejich četnost. Díky počítačům sice generujeme další a další prvočíselná dvojčata, to však ale není důkaz. Přesný důkaz stále nebyl formulován.
Pierre Fermat se domníval, že všechna čísla ve tvaru Fm = 2k + 1, kde k = 2m, m = 0, 1, 2, ... jsou prvočísla. Prvních pět členů této posloupnosti 3, 5, 17, 257, a 65 537 prvočísla skutečně jsou. Avšak už v roce 1732 Leonhard Euler zjistil, že šesté číslo 4 294 967 297 je složené, protože je dělitelné 641. Tato čísla se nazývají Fermatova čísla. V současné době je počet Fermatových prvočísel stále otevřeným problémem, předpokládá se, že kromě prvních pěti už žádná další prvočísla nejsou.
Marin Mersenne studoval čísla ve tvaru Mp = 2p – 1, kde p je prvočíslo. Jestliže je i Mp prvočíslo, nazývá se Mersennovo prvočíslo. Původně se myslelo, že pro každé prvočíselné p vyjde Mersennovo prvočíslo, ale v roce 1536 tuto domněnku vyvrátil Hudalricus Regius pro p = 11. Do dneška bylo nalezeno jen 48 Mersennových prvočísel. (pro p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, až po největší 57 885 161, které bylo objeveno v roce 2013). Těmito čísly se zabýval i Pierre Fermat a jeho výsledky ho dovedly k objevu Malé Fermatovy věty, která říká, že prvočíslo q dělí (beze zbytku) rozdíl 2q – 1 – 1.
Vzorec na výpočet prvočísel přinesl i Leonhard Euler ve tvaru n2 + n + 41. Platí pro každé celé číslo od 0 až po 39. Podobně můžeme některá prvočísla vypočítat i podle vztahu n2 + n + 17, který dává prvočísla pro n od 0 do 15. Prvočísla získáme i pomocí faktoriálu ze vztahu n! + 1 pro n = 1, 2, 3, 11, 27, 37, 41, 73, 77, 116, 154, 320, 340, 399, 427, 872 a dosud nejvyšší prvočíslo tohoto typu je pro n = 1477.
Použité zdroje:
[1] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[2] CRILLY, T. Velké otázky. Matematika. Praha: Knižní klub, 2012. 1. vydání. ISBN: 978-80-242-3596-7.
[3] ČIŽMÁR, J. Matematika pro 6. ročník I. díl. Praha: Prometheus, 1995. ISBN 80-85849-81-X.
[4] ERBAN, R. Prvočísla, přednáška s čokoládou. Matematický korespondenční seminář.
[5] SPENCER, A. Kniha čísel. 1. vydání. Praha: Albatros, 2005. ISBN: 13-805-KMČ-005.
[6] STEWART, I. Kabinet matematických kuriozit profesora Stewarta. Praha: Dokořán, 2013. ISBN 978-80-7363-292-2.