Magické mohou být i jiné útvary, např. magický šestiúhelník existuje jen jeden o velikosti strany 3. Jsou v něm umístěna čísla 1 až 19 a součet každé strany a úhlopříčky je 38.

To platí jen pro tzv. normální šestiúhelníky, které obsahují po sobě jdoucí celá čísla začínající 1, 2, 3 …. Pokud ustoupíme od poslední podmínky (budeme do magického šestiúhelníku vpisovat čísla začínající od čísla vyššího, např. 3, 4, 5 …), existuje variant víc. Zatím největší takový magický šestiúhelník nalezl Zahray Arsen v roce 2006 a velikost jeho strany je 7, obsahuje čísla 2 až 128 a jeho konstanta je 635.
Další variantou je magická Davidova hvězda. Existuje celkem 80 variant, jejichž každá řada dává součet 26 (řešení vlevo). Můžeme navíc požadovat, aby i součet čísel v šesti vrcholech dával 26. Toto řešení je až na pootočení jediné (řešení vpravo).


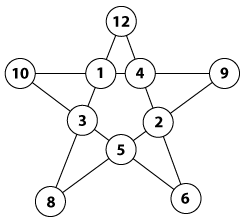
Magická může být i pěticípá hvězda, kde součet každých čtyř čísel ležících v jedné přímce je roven 24. I když její magičnost je trošku narušena tím, že jsou zde vepsaná čísla od 1 do 12 ale s vypuštěním číslic 7 a 11. Pro pěticípou hvězdu totiž pravé magické řešení neexistuje.
Použité zdroje:
[1] BÁLINTOVÁ, A. – TROJÁČKOVÁ, R. Sudoku a história magických štvorcov. Sborník sylabů 31. mezinárodní konference historie matematiky, Velké Meziříčí 18. – 22. 8. 2010. Matfyzpress, Praha 2010.
[2] CRILLY, T. Matematika. 50 myšlenek, které musíte znát. 1. vydání. Praha: Slovart, 2010. ISBN: 978-80-7391-409-7.
[3] FUCHS, E. Magické čtverce aneb Od Knihy I-t´ing k internetové současnosti.
[4] PRADLOVÁ, J. O čem přemýšlí Dürerův anděl aneb magický čtverec z Fibonacciho čísel. Matematika-Fyzika-Informatika. Roč. 11, únor 2002, č. 8, s. 321-328.
[5] SPENCER, A. Kniha čísel. 1. vydání. Praha: Albatros, 2005. ISBN: 13-805-KMČ-005.
[6] STEWART, I. Kabinet matematických kuriozit profesora Stewarta. Praha: Dokořán, 2013. ISBN 978-80-7363-292-2.
[7] STEWART, I. Truhlice matematických pokladů profesora Stewarta. Praha: Dokořán, 2013. ISBN 978-80-7363-527-5.
