Teorie
Uvažujme potrubí, které se v určitém místě sužuje. Tady dojde k nárůstu rychlosti, ale co se stane s tlakem?
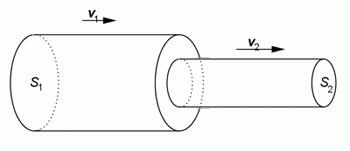
Veličiny popisující proudění vody v různých částech potrubí lišících se průměrem.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Tento problém poprvé formuloval Daniel Bernoulli.
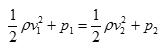
Bernoulliho rovnice vyjadřuje zákon zachování energie ideální kapaliny proudící ve vodorovné trubici. Platí i pro plyny. Ty ale při malé změně teploty mění své fyzikální vlastnosti – hustotu, viskozitu apod. a navíc na rozdíl od kapalin jsou stlačitelné.
Daniel Bernoulli.
Zdroj: Techmania Science Center. Autor: Pavel Trnka. Under Creative Commons.
Základní tvar Bernoulliho rovnice platí jen pro ideální kapaliny, kde je průtok beze ztrát. Pro reálnou kapalinu se Bernoulliho rovnice doplňuje o ztrátovou výšku. Ke ztrátám dochází díky tření o stěny nádoby díky náhlé změně směru proudící kapaliny.
Z Bernoulliho rovnice vyplývá, že tlak proudící kapaliny klesá s rostoucí rychlostí. Při velkém zúžení trubice, kde rychlost proudu kapaliny značně vzroste, může tlak v kapalině klesnout tak, že bude menší než tlak atmosférický – v zúženém místě trubice vzniká podtlak. Jestliže v této zúžené části bude otvor, pak bude z okolí nasávat vzduch. Tento jev se také nazývá hydrodynamické paradoxon. Podtlak u proudícího vzduchu se využívá např. u rozprašovače, stříkací pistole, karburátoru nebo vodní vývěvy.
Na základě Bernoulliho rovnice můžeme vysvětlit „přitahování“ dvou rovnoběžně plujících lodí. Když plují dvě lodě spolu rovnoběžně, vzniká mezi jejich boky jakýsi kanál, v němž je v klidu voda a pohybují se stěny. V zúžené části kanálu proudí voda rychleji a působí na stěny – lodě menším tlakem. Ale na vnější stěny působí voda tlakem větším. Důsledkem je přibližování obou lodí.
Podobně funguje i exponát Míčky. Jestliže do proudu vody vložíme míček, pak se na jeho ploše vytvoří velmi tenký vodní film, vrstva vody se tedy zúží a tím i zrychlí. Podle Bernoulliho rovnice dojde ke snížení tlaku a chycení míčku do vodní pasti.
