U mnoha atomů včetně atomu vodíku se při použití spektrometrů s vyšším rozlišením začala pozorovat tzv. jemná struktura spekter, ukázalo se, že některé spektrální čáry jsou ve skutečnosti skupiny blízkých čar. Proto s jedním z prvních pokusů o vylepšení Bohrova modelu přišel Arnold Sommerfeld, když nahradil Bohrovy kruhové dráhy eliptickými. Pak musel k hlavnímu kvantovému číslu n přidat i vedlejší kvantové číslo l. Hlavním kvantovým číslem je určena velká poloosa a = n2r1 a vedlejším kvantovým číslem malá poloosa a´ = n (l + 1)r1. Aby v krajním případě přešla elipsa v kružnici, je třeba, aby n = l + 1, proto vedlejší kvantové číslo může nabývat maximální hodnoty n - 1. Nejmenší možná hodnota je 0.
Teoretické zdůvodnění vedlejšího kvantového čísla na základě kvantové teorie podla Wernera Heisenberga, který opravil původní Bohrovu podmínku pro kvantování momentu hybnosti elektronu (b = ħn) a vyjádřil jej novou rovnicí
![]()
Z této podmínky plyne trošku jiný závěr než z Bohrovy. Hlavnímu kvantovému číslu n přísluší n kvantových drah, lišících se navzájem hodnotou vedlejšího kvantového čísla l, a tedy i tvarem dráhy elektronu. Čím nižší je vedlejší kvantové číslo, tím je eliptická dráha výstřednější. Dráhy se stejným vedlejším kvantovým číslem se pak označují písmeny podle schématu
l: 0, 1, 2, 3, …
písmeno: s, p, d, f, …
Písmena s, p, d, f se píší za hlavní kvantové číslo, takže mluvíme např. o stavu 1s, 2s, 3d atd. Písmena pocházejí z klasifikace spekter na série, nazývané v angličtině sharp, principal, diffuse a fundamental (ostrá, hlavní, difúzní a základní), které se používaly před rozvojem atomové teorie. Orbitální kvantové číslo slouží ke kvantování momentu hybnosti elektronu. Kombinace hlavního kvantového čísla s písmenem reprezentujícím orbitální moment hybnosti tvoří vhodné a užívané označení atomových stavů. Symbolické označení stavů atomu vodíku
|
|
s l = 0 |
p l = 1 |
d l = 2 |
f l = 3 |
g l = 4 |
h l = 5 |
|---|---|---|---|---|---|---|
|
n = 1 |
1s |
|
|
|
|
|
|
n = 2 |
2s |
2p |
|
|
|
|
|
n = 3 |
3s |
3p |
3d |
|
|
|
|
n = 4 |
4s |
4p |
4d |
4f |
|
|
|
n = 5 |
5s |
5p |
5d |
5f |
5g |
|
|
n = 6 |
6s |
6p |
6d |
6f |
6g |
6h |
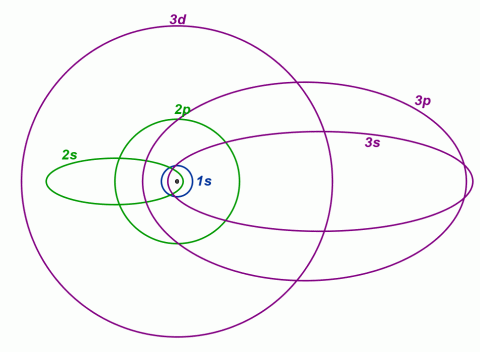
Tvar dráhy jednotlivých elektronů v měřítku podle Sommerfeldova modelu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Zavedení vedlejšího kvantového čísla nepostačuje k vysvětlení jemné struktury spektrálních čar. Sommerfeld ale přihlédl k měnící se rychlosti na eliptické dráze – v bodě nejbližším jádru je největší a v bodě nejbližším jádru je nejmenší. Protože se elektron po své dráze pohybuje velkou rychlostí blížící se rychlosti světla, tak Sommerfeld ve svém modelu změnil hmotnost elektronu v souladu s teorií relativisty. Elektron má tedy největší hmotnost nejblíž u jádra a nejmenší hmotnost nejdál od jádra. Vlivem změn hmotnosti elektronu se dráha v nejbližším bodě víc zakřivuje a to vede k přemisťování celé dráhy, která nabývá tvar růžice. Proto se poněkud liší energie elektronu na drahách se stejným hlavním kvantovým číslem a s odlišným vedlejším kvantovým číslem. Rozdíl energií elektronu na jednotlivých drahách vede k rozštěpení spektrálních čar.
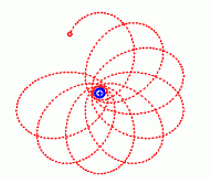
Tvar dráhy elektronu vlivem změn hmotnosti elektronu.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Uvedený model dokázal objasnit jemnou strukturu spekter pouze částečně, nedokázal např. objasnit dublety (dvojice blízkých čar), které souvisí s existencí spinu elektronu. Ukázalo se, že představa pohybu elektronu s určitou hybností po určité dráze je neudržitelná. Energetické spektrum získané na základě Sommerfeldova modelu zahrnuje z relativistických korekcí pouze relativistickou hmotnostní korekci. Spektrum je analogické se spektrem získaným řešením Kleinovy–Gordonovy rovnice, což je relativistická vlnová rovnice, nezahrnující spin částic.
Existují jevy, na které je Bohrova teorie krátká, její předpovědi selhávají např. při vysvětlení ohybu elektronů. Představy o makroskopických jevech nelze aplikovat na jevy uvnitř atomů. Nicméně se lze do jisté míry držet domněnky o oběžných drahách elektronů uvnitř atomu, protože často vede k přibližně správným výsledkům, které v souladu s experimenty vyžadují drobné korekce. Proto k vysvětlení řady jevů použijeme Bohrův-Sommerfeldův model atomu.
