Na základě Lorentzovy transformace spojil Hermann Minkowski v roce 1908 prostor a čas v jeden celek. Každá bodová okamžitá událost je určena čtyřmi veličinami: třemi souřadnicemi x, y, z, které stanovují polohu bodu v prostoru, a příslušným časem t. Nebo obráceně: každý bod prostoru reprezentuje jednu událost. Měřítkem takového systému je rychlost světla, která je ve všech systémech stejná. Aby rozměr všech veličin byl stejný, zavedl Minkowski místo času t vzdálenost, kterou urazí světlo za tuto dobu, tedy veličinu ct. Označil ji jako čtvrtou souřadnici imaginární veličinou ict. Podle toho je pak svět čtyřrozměrným geometrickým souborem bodů a mezi jeho souřadnicemi platí
![]()
Minkowského prostoročas můžeme znázornit pomocí světočar, tj. drah částice v časoprostoru. I když je částice v klidu vzhledem k dané inerciální vztažné soustavě, přesto v Minkowského prostoročasu odpovídá částici přímka rovnoběžná s časovou osou. Představme si dvě události pro jednoduchost odehrávající se jen v rovině, kde se mění souřadnice x a ct. Událost 1 nastane pro x = 0 a t = 0, událost 2 při x = Δx a t = Δt. Interval Δs mezi nimi je definován vztahem
![]()
Jaké budou závislosti mezi událostmi 1 a 2? Událost 2 může mít nějakou příčinnou souvislost s událostí 1 za předpokladu, že signál šířící se pomaleji než světlo může tyto události spojovat
![]()
Interval, pro který je (Δs)2 > 0, se nazývá časový. Každý časový interval, spojující událost 1 s jinou událostí, leží uvnitř světelného kužele ohraničeného přímkami x = ct a x = –ct. Všechny události, které by mohly ovlivnit událost 1, leží uvnitř světelného kužele směřujícího do budoucnosti.
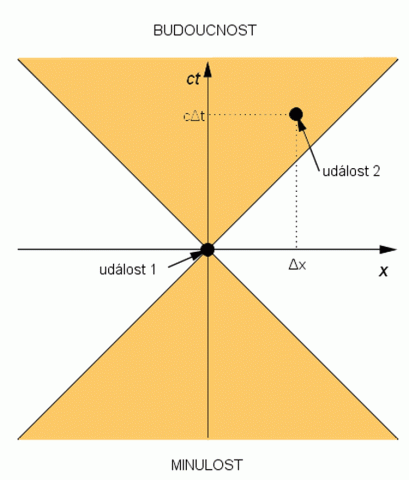
K výkladu pojmu prostoročas.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Kriteriem neexistence jakékoli příčinné souvislosti mezi událostmi 1 a 2 je nerovnost
![]()
Interval, pro který (Δs)2 < 0, se nazývá prostorový. Každá událost, která je spojena s událostí 1 prostorovým intervalem, leží vně světelného kužele události 1 a nemohla interagovat s událostí 1 v minulosti a nebude s ní moci interagovat ani v budoucnosti. Takovéto události jsou bez jakékoli souvislosti.
Jestliže události 1 a 2 mohou být spojeny světelným signálem, pak
![]()
Interval, pro který (Δs)2 = 0, se nazývá světelný. Události, jež mohou být spojeny s událostí 1 světelným intervalem, leží na povrchu světelného kužele.
