Při otáčivém pohybu tuhého tělesa kolem nehybné osy opisují body tělesa kružnice, jejichž středy leží na ose otáčení. Úhlová rychlost w pohybu je pro všechny body tělesa stejná, velikosti rychlostí jednotlivých bodů jsou přímo úměrné jejich vzdálenosti od osy otáčení. Kinetickou energii obruče o poloměru r otáčející se kolem středu vypočítáme
Všimněte si, že kinetická energie nezávisí jen na úhlové rychlosti otáčení a na hmotnostech tělesa, ale také na vzdálenostech od osy otáčení. Výraz mr2 se nazývá moment setrvačnosti vzhledem k ose otáčení a označuje se písmenem J. Jednotkou momentu setrvačnosti je kg m2. Kinetickou energii libovolného tělesa otáčejícího se kolem nehybné osy můžeme vyjádřit pomocí momentu setrvačnosti
Tak jako potřebujeme více energie, abychom dali do pohybu hmotnější těleso potřebujeme více energie, abychom dali do rotačního pohybu těleso s větším momentem setrvačnosti. Máme-li dvě kola o stejné hmotnosti, mají stejnou setrvačnost, pokud vykonávají pouze posuvný pohyb. Nemají však stejný moment setrvačnosti, neboť ten je závislý na rozložení hmotnosti kola. Pro kolo, které má svoji hmotnost rozloženou po obvodu kola, je těžší dostat se do rotace než pro kolo, které má svoji hmotnost rozloženou rovnoměrně nebo u středu. Proto se bude prstenec otáčet pomaleji než disk.
Libovolný pohyb tělesa si můžeme představit složený z posuvného pohybu a z otáčivého pohybu kolem osy, procházející těžištěm tělesa. Kinetická energie tělesa je pak dána součtem energie posuvného pohybu a energie otáčivého pohybu kolem osy jdoucí těžištěm
Moment setrvačnosti závisí na rozměrech a tvaru tělesa a na poloze osy otáčení vzhledem k tělesu. Nejsnadněji lze vypočítat moment setrvačnosti stejnorodých souměrných těles vzhledem k ose otáčení procházející těžištěm. Momenty setrvačnosti některých těles jsou v následující tabulce.
|
Tenká obruč o hmotnosti m a poloměru R |
|
|
Plný stejnorodý válec |
|
|
Plná stejnorodá koule |
|
|
Stejnorodá tyč délky l vzhledem k ose kolmé k tyči a jdoucí jejich středem |
|
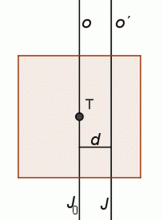
Známe–li moment setrvačnosti J0 vzhledem k ose o jdoucí těžištěm, můžeme snadno vypočítat moment setrvačnosti vzhledem k rovnoběžné ose ợ, jejíž vzdálenost od osy jdoucí těžištěm je d.
Ke Steinerově větě.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Vztah mezi oběma momenty setrvačnosti vyjadřuje Steinerova věta
Moment setrvačnosti tělesa vzhledem k ose neprocházející těžištěm si můžeme představit složený ze dvou částí: z momentu setrvačnosti J0 vzhledem k ose procházející těžištěm a z výrazu md2.
Pomocí momentu setrvačnosti můžeme definovat i moment hybnosti L vzhledem k pevné ose, pro který platí
kde J je moment setrvačnosti a ω je úhlová rychlost. Máme-li rotující tuhé těleso, závisí jeho moment setrvačnosti na rozložení hmoty v tělese. V případě různých těles o stejné hmotnosti bude největší moment setrvačnosti u tělesa, jehož hmota je umístěna dále od osy otáčení. Obecně moment setrvačnosti závisí na hmotnosti m a druhé mocnině vzdálenosti R od osy otáčení. Pokud bychom nahradili krasobruslaře plným válcem, pak můžeme vztah pro moment hybnosti přepsat
Moment setrvačnosti závisí na rozměrech a tvaru tělesa a na poloze osy otáčení vzhledem k tělesu. Přitiskne-li krasobruslař v piruetě roztažené ruce k tělu, zmenší svůj poloměr na polovinu a tím i moment setrvačnosti. Jestliže má zůstat moment hybnosti jeho těla zachován, musí se současně zvětšit uhlová rychlost rotace čtyřikrát. Pokud chce piruetu rychle ukončit, postupuje obráceně. Obdobně se chová při skoku s rotací, zvláště čtverném, protože čas pro osm rotací volně nad ledem má omezený.
