Nejstarší zpodobnění míry je asi délková míra na soše Gudey z Lagaše uložené ve sbírkách Louvru v Paříži, která zpodobňuje sumerského vládce v Uru, staré téměř pět tisíc let. Potřeby měření a vážení (které se dlouho uvádělo zvlášť) se postupně zvětšovaly, počet měřených veličin však rostl pomalu. Prvními měřenými veličinami byl čas, úhly, délka, plošný obsah a objem. Až na konci 17. století především díky fyzice začal růst počet měřených veličin. Na konci 18. století vznikl Metrický systém, které byl v průběhu 19. století zaváděn do praxe. V Čechách byl garantem Úřad pro míry, váhy a drahé kovy, který byl v roce 1960 začleněn do Úřadu pro normalizaci a měření, který se dnes jmenuje Úřad pro technickou normalizaci, metrologii a státní zkušebnictví.
Při měření porovnáváme veličinu, jejíž číselnou hodnotu neznáme s jednotkou vhodnou pro měření této veličiny. Měřením fyzikální veličiny rozumíme určení její číselné hodnoty v daných jednotkách. Měření probíhá zpravidla ve třech etapách: příprava měření, vlastní měření a zpracování výsledků měření. Při měření se projevují chyby náhodné (způsobené např. špatným nastavením počátku měřidla či špatným úhlem pohledu na měřítku) a soustavné (způsobené použitím nesprávného měřidla, či vadným měřidlem, nesprávnou metodou apod.). Soustavné chyby můžeme vyloučit použitím různých metod a různých měřících přístrojů.
Vliv náhodných chyb se sníží opakovaným měřením. Při mnoha měřeních stejné veličiny se náhodné chyby vyrovnají. Z tohoto předpokladu vychází výpočet aritmetického průměru z naměřených hodnot x1 až xn veličiny x, který považujeme za její nejpravděpodobnější hodnotu
![]()
kde n je počet měření. Výsledky měření zaokrouhlujeme podle platných pravidel. Žádný konečný výsledek by obecně neměl být zapsán číslem s větším počtem platných míst, než měly výchozí údaje (měření).
Zjistíme odchylky Δn jednotlivých naměřených hodnot od průměru
![]()
Určíme směrodatnou odchylku (tzv. absolutní chybu)
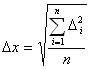
Výsledný rozměr pak zapíšeme ve tvaru
![]()
Budeme–li třeba měřit rozměr d nějaké součástky, zapíšeme pak výsledek do tvaru d = (36,5 ± 0,3) mm. Znamená to, že tento rozměr jsme určily přibližně v rozmezí 36,2 mm až 36,8 mm.
Často je určení absolutní chyby nedostatečné. Jestliže změříme délku drátu 100,00 cm a průměr drátu 0,5 mm se stejnou absolutní chybou 0,1 mm, není průměr určen dostatečně přesně. O tom nás přesvědčí relativní chyba
![]()

